Circle inversion

and a proof of Ptolemys' Theorem

Jul 18, 2024

This Viewpoint takes a look at Geometric INVERSION - a powerful technique for solving various problems and one rarely covered in school courses even at “A” level.1 The Viewpoint also shows how inversion provides an elegant proof of Ptolemy’s Theorem - (earlier Viewpoint).

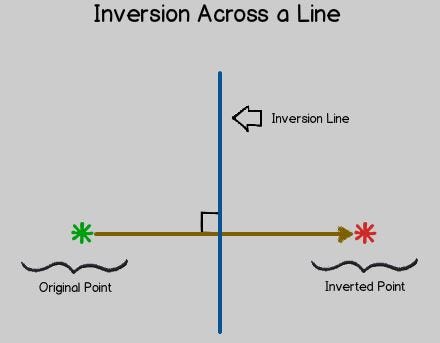
The next image shows a vertical blue line - labelled Inversion Line. If the green point to the left is “inverted”, it becomes the red point to the right. In this case, the inversion is essentially a reflection. The inversion of the red point is, of course, the green point. The red point and green point are equidistant from the blue line.

Inversion with respect to a circle

The more usual geometric situation is inversion with respect to a reference circle.

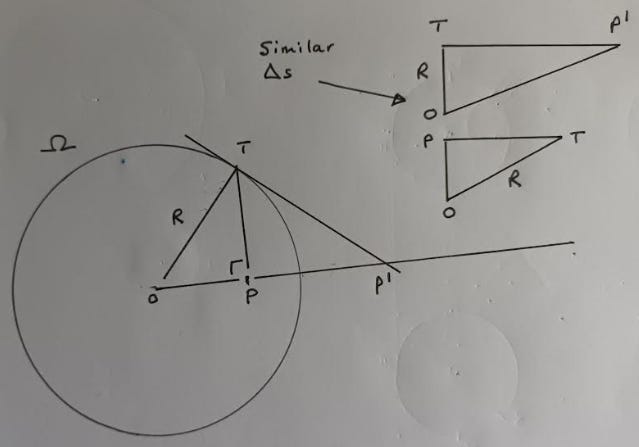
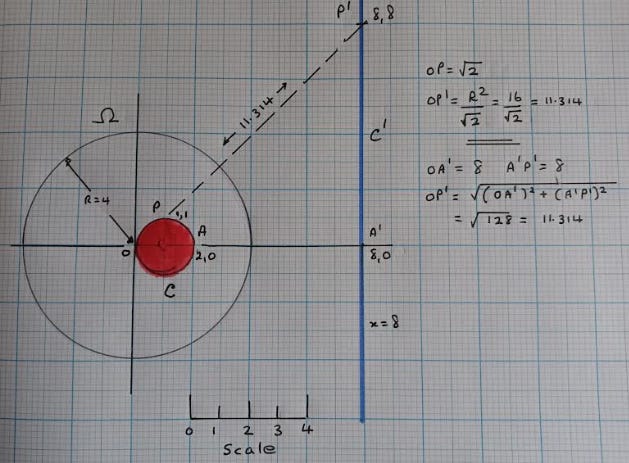
In the next diagram, P is a point inside reference circle Ω with centre O and radius R units. A “ray” is drawn from O through P and outwards beyond the circumference of Ω. PT is a straight line at right angles to OP and intersects the circumference of Ω at T. O is joined to T and a tangent to the circle is drawn at T. This tangent cross the “ray” at point P^Iand that is the inverse of point P with respect to the circle. The inverse of P^Iis P.

Note that there are two similar triangles OPT and OTP^Iand from those triangles

OP^I / R = R / OP and therefore OP.OP^I = R²

That is the formula for circle inversion.

Using the formula, any point (such as P) within the circle can be mapped to a point P¹ outside the circle (and vice versa).

If P is a point on the circumference of Ω then the inversion of P is the same point. In other words, points on the circumference of the reference circle are invariant under inversion.

As point P gets closer to the centre of the reference circle Ω, the inversion of P gets increasingly distant from Ω - the distance tends to infinity.2

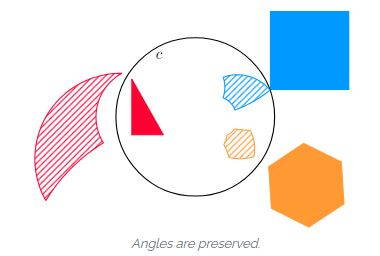
Shapes can be inverted by inverting points on the boundary of the shape. A very important property of this type of inversion is that angles are preserved. As a consequence of angle preservation, objects that are tangential to each other, are inverted to objects that are also tangential to each other.

A circle, inverts to a circle.

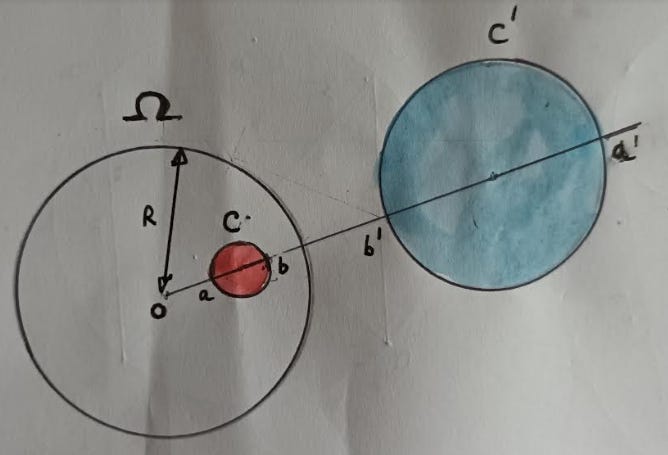
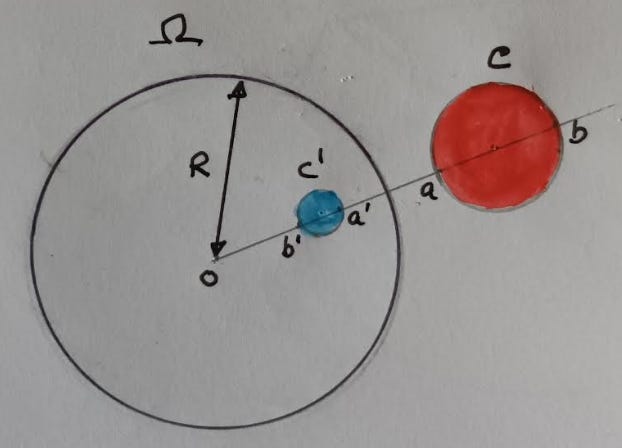
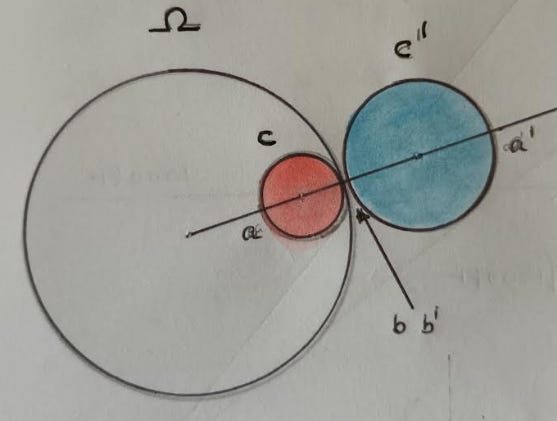
In the next diagrams, the reference circle is Ω and the circle to be inverted is C (shown red). The resulting inversion is C¹(coloured blue).

Example 1] C within the reference circle inverts to C¹outside Ω

Example 2] C outside the reference circle inverts to C¹inside Ω

Example 3] C inside and tangential to the reference circle inverts to C¹outside and tangential to Ω - (the point of tangency b b¹is invariant

Example 4] If the circle to be inverted C touches the centre O of the reference circle Ω then C inverts to a straight line C¹ (shown in blue). (The straight line is regarded by some mathematicians as a circle with infinite radius. Adopting that view enables them to say that circles always invert to circles).3

Proof, using inversion, of Ptolemy’s Theorem

Ptolemy’s theorem is that, for a cyclic quadrilateral (vertices A, B, C, D)

AB.CD + AD.BC = AC.BD (see (earlier Viewpoint).

The following proof uses inversion and also the properties of similar triangles.

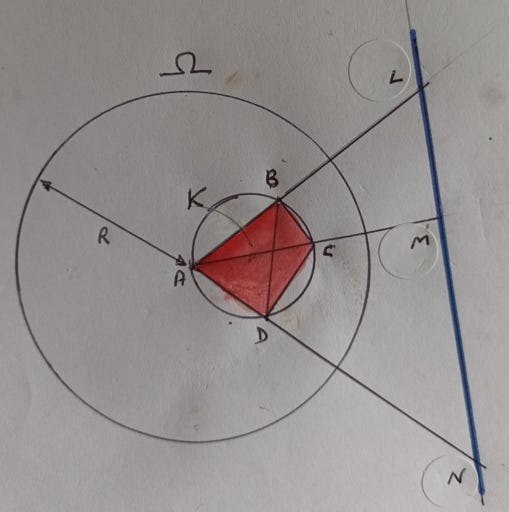
The next diagram shows a cyclic quadrilateral ABCD (coloured red) within a circle (K) and K is within the reference circle Ω (of radius R). Point A is both a vertex of the quadrilateral and the centre of the reference circle. This fact means that the inversions of points B, C and D lie on a straight line (coloured blue). The inversions of B, C and D are shown as L, M and N respectively.

Step 1 - From the definition of inversion AB.AL= R² and AC.AM= R² and AD.AN= R²

Step 2 - Triangles ABC and AML are similar because AB.AL = AC.AM from which AB / AC = AM / AL and also angle CAB is common to both triangles.

The same reasoning tells us that triangles ADC and AMN are similar and triangles ABD and ANL are also similar.

Step 3 - Find expressions for the lengths LM , MN and LN

Because of similarity between triangles ABC and AML

LM / BC = AL / AC and therefore LM = (BC . AL) / AC

but AB.AL= R² and so LM = (BC.R²) / AB.AC

Applying the same reasoning to triangles ADC and AMNshows that

MN = (CD.R²) / AC.AD

and, for triangles ABD and AD¹ B¹

LN= (BD.R²) / AD.AB

Step 4 - Note that LM + MN= LM and so

(BC.R²) / AB.AC + (CD.R²) / AC.AD = (BD.R²) / AD.AB

Step 5 - Simplify

Divide both sides by R² gives

BC / AB.AC + CD / AC.AD = BD / AD.AB

Now multiply both sides by AB.AC.AD and with slight-re-arrangement

AB.CD + AD.BC = AC.BD

which proves Ptolemy’s theorem for the cyclic quadrilateral ABCD.

Many other proofs of Ptolemy’s theorem are available but the proof by inversion has a particular elegance. Here is another proof using complex numbers