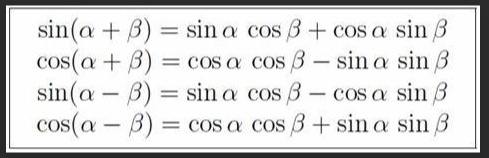Ptolemy's Theorem
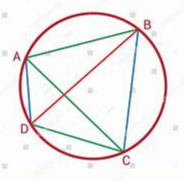
Claudius Ptolemy (c. 100 CE - c.170CE) was an Alexandrian mathematician, astronomer, and geographer. His name is given to a theorem in Euclidean geometry which relates the side lengths of a CYCLIC quadrilateral to the lengths of its diagonals. A CYCLIC quadrilateral is one which is exactly inscribed in a circle - e.g. quadrilateral ABCD in this figure. It is easy to see that any rectangle is also a cyclic quadrilateral.
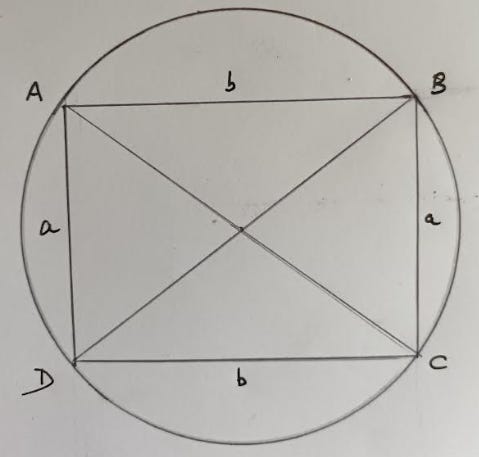
The next diagram shows a RECTANGLE within a circle. The side lengths of the rectangle are a and b units.
Applying the Pythagorean Theorem … AC2 = a2 + b2 = and so AC = √(a2 + b2)
Similarly BD = √(a2 + b2) from which AC x BD = a2 + b2
Next, note that AD x BC = a2 and AB x CD = b2 and so it follows that
AD.BC + AB.CD = AC.BD
This result, proved here for a cyclic rectangle, is a special case of PTOLEMY’s THEOREM which states
For any cyclic quadrilateral, the product of its diagonals is equal to the sum of the product of each pair of opposite sides
A video illustrating one proof of the theorem is - A Beautiful Proof of Ptolemy's Theorem. It is by no means the only proof - see, for example, A collection of proofs of Ptolemy’s Theorem | Chaitanya's Random Pages (wordpress.com).
See also An Easy Proof of Ptolemy’s Theorem and Ptolemy's Theorem Cyclic quadrilateral (gogeometry.com)
The Converse?
A converse is a theorem in reverse. Take a theorem written IF this, THEN that. The converse is IF that, THEN this.
An attractive thought might be that if a theorem is proved, its converse must also be correct but is that the case? The answer is NOT necessarily. In mathematics, a converse statement has to be proved.
The Pythagorean Theorem is true. The converse says that, if the square of two sides of a triangle sum to the square of the third side, then the triangle is right-angled (and the right angle is in between those first two sides). This converse can be proved to be true. See the discussion at - The converse of Pythagoras' theorem.
The converse of Ptolemy’s theorem is - for a quadrilateral, if the sum of the products of its two pairs of opposite sides is equal to the product of its diagonals, then the quadrilateral can be inscribed in a circle. It has been proved that this converse is true.
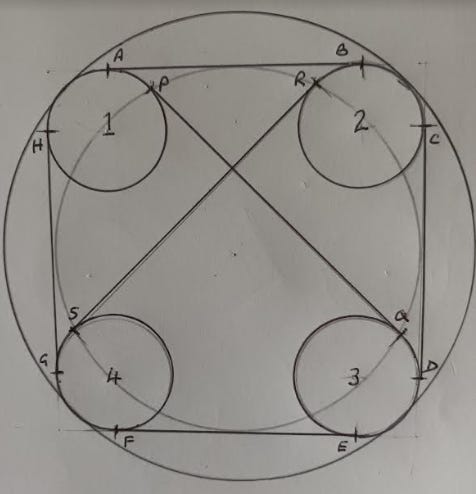
The placemat
Imagine a “placemat” with rounded corners - see diagram. The mat lies within a large circle such that the rounded corners of the mat are tangential to the circle. The rounded corners are formed from circles 1, 2, 3 and 4 which all have equal radii. The straight sides of the mat are tangential to the corner circles - e.g. AB is tangential to circle 1 and circle 2. Further, AB = CD = EF = GH. Diagonals are drawn which are tangential to circles 1,3 and circles 2,4.
Careful drawing and measurement shows that AB.EF + CD.GH = PQ.RS but that does not constitute mathematical proof.
Proof exists and is the work of Irish mathematician John Casey (1820 - 1891).
Exercise: Prove that the points P, R, Q, S lie on a circle so that PRQS is a cyclic quadrilateral. Clue: If PR.QS + RQ.PS = PQ.RS then, by the converse of Ptolemy’s theorem, PRQS is cyclic.1
Casey’s Theorem
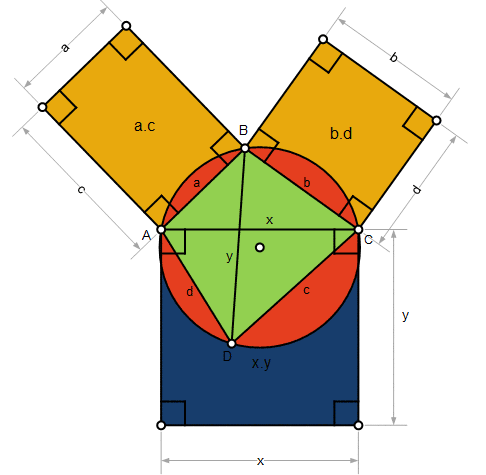
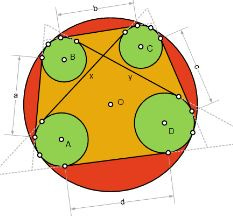
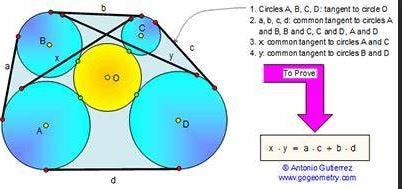
Casey’s theorem (shown in the placemat problem) is a generalised form of Ptolemy’s theorem. The next diagram illustrates the theorem.
The large circle (red) contains 4 non-overlapping circles (A, B, C, D shown in green) and those circles are tangential to the large circle. Tangents are drawn from A to B, B to C, C to D and D to A and the tangent lengths are, respectively, a, b, c, d. Tangents (lengths x and y) are drawn diagonally from A to C and from B to D.
Casey's theorem is that a.c + b.d = x.y
Casey’s theorem can be extended to other cases such as where the circles A, B, C, D lie outside the larger circle.
You can “play” with Casey’s Theorem on Geogebra - Casey's theorem – GeoGebra
See also Gogeometry.com and Casey's Theorem: Generalized Ptolemy's Theorem.
Brahmagupta
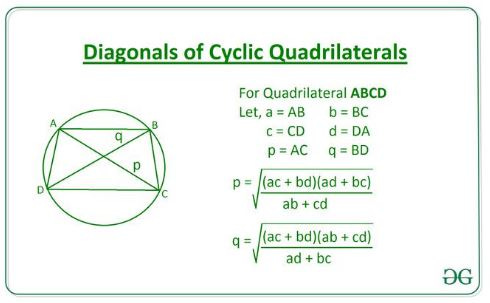
The Indian mathematician Brahmagupta (598 - 668 CE) produced particularly notable results including calculation of the lengths of the diagonals of cyclic quadrilaterals. The formula, applicable to a convex cyclic quadrilateral, is
See Ptolemy's Theorem Extension Ratio of Diagonals Cyclic quadrilateral: Antonio Gutierrez (gogeometry.com)
Art of Problem Solving - Brahmagupta’s formula
Brahmagupta-Mahavira Identities (cut-the-knot.org)
Trigonometry
Ptolemy’s Theorem also links to trigonometry.
Ptolemy's sum and difference formulas (clarku.edu)
Quadrilaterals
Quadrilaterals may be either convex or concave
Cyclic quadrilateral - the four vertices lie on a circumscribed circle. A convex quadrilateral is cyclic if and only if opposite angles sum to 180°.
Cyclic quadrilateral - Wikipedia
Cyclic Quadrilateral (Theorems, Proof & Properties) (byjus.com)
Quadrilaterals Revealed (uga.edu)
Definitions and Hierarchy of Quadrilaterals - Department of Mathematics at UTSA
Additional Links
Ptolemy's Theorem (cut-the-knot.org)
What Is Ptolemy's Theorem? » ScienceABC
The History of Mathematics - Ptolemy’s theorem (unsw.edu.au)
Casey theorem - MacTutor History of Mathematics (st-andrews.ac.uk)
Quadrilateral -- from Wolfram MathWorld
The placemat is designed to have symmetry from which it can be deduced that PR is parallel to QS. The quadrilateral PRQS has two equal sides PS and RQ and also its diagonals (PQ, RS) are equal. With those facts, it can be shown that PR.QS + RQ.PS = PQ.RS. From there, due to the converse of Ptolemy’s theorem, it is proved that PRQS is cyclic.