Jacob Bernoulli (1655 - 1705) was a member of a notable family which also included Daniel Bernoulli (1700 - 1782) who formulated the ‘Bernoulli Principle’ explained at Principles of Flight: Bernoulli's Principle (nasa.gov).
Jacob Bernoulli is noted for his study of compound interest and the discovery of the strange number expressed today simply as e. It has an approximate value of 2.71828 and, like Pi (π), it is an irrational number. The decimal places can extend forever.
The symbol e was given to this number by Leonard Euler (1707 - 1783) but it is not thought that Euler did this to claim the number for himself. Euler took Bernoulli’s work forward and found a method of computing e involving an “infinite series” but let’s avoid that for now.1
Bank with us - 100% interest rate:
We would never see an advert like that since typical interest rates are well under 10%. But imagine the Bank of Generosity which pays 100% per annum and a saver deposits a single currency unit (e.g. £1 or $1 etc). After 1 year interest is paid and the saver now has 2 currency units.
The bankers then change the system so that the 100% over the year is paid in two instalments - 50% after 6 months and 50% after 12 months. Is the saver better off? Yes - he then has 2.25.
Suppose they decided to pay a twelfth of the interest every month - (i.e. 12 times a year). Our saver would end up with 2.61.
Paying this weekly would improve matters further for the saver who after 52 weeks would have 2.69.
If it were to be paid daily (365 times a year) then the amount saved would be £2.71.
This process could be continued until. ultimately, interest was paid continuously.
What can be readily seen is that the amount our saver has after a year is converging to some amount just over 2.71.
All of this is well explained in this video …..
A crucial characteristic of e is that it is a number that does not arise from some geometric shape such as a circle. It is a number that arises naturally in connection with growth and decay.
In everyday language the phrase exponential growth is used to describe rapid expansion or contraction but a mathematician would then wish to know exactly how the growth or decay was occurring. A useful explanation of the terms is at -Exponential growth: what it is, why it matters, and how to spot it - The Centre for Evidence-Based Medicine (cebm.net)
A straightforward example of rapid growth is something that doubles at particular times (e.g. daily). This is the The Rice and Chessboard Legend where, on Day 1, a single grain of rice is placed on the first square of the chessboard. On Day 2, two grains are placed on square 2. This “doubling” continues up to Day 64. A doubling process like this is an example of a geometric series.
Euler’s number e appears frequently in problems connected with growth and decay and some examples are shown at 17 Exponential Growth Examples in Real Life – StudiousGuy.
An important graph:
The idea of “powers” (or exponents / indices) is familiar enough. For instance if A = 2, then powers of A can be derived - e.g.
A2 = 2 x 2 = 4
A3 = 2 x 2 x 2 = 8
A4 = 2 x 2 x 2 x 2 = 16
21.7 = 3.24901
2e = 6.58089 and so on.2
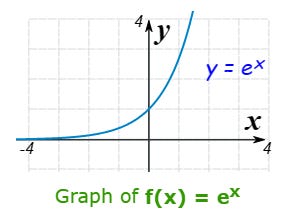
If we take Euler’s number e and raise it to powers and then graph the results, the outcome looks like this -
This function y = ex (e to power x) has some important properties such as the slope of the blue line. The slope shows the rate of change of y at any given point on the graph. The steeper the line, the greater the rate of change.
At all points on this graph, the rate of change can be proved to be equal to ex so, for instance, when x = 0 the function is y = e0 and raising any number to power 0 produces the answer 1.
Another example is when x = 1. y is then e1 and any number raised to power 1 is simply the original number. Hence, when x = 1 the value of y is e.
Looking into questions of rate of change led mathematicians to differential calculus and its counterpart - integral calculus.
Thank you for reading this. Comments are welcome and please consider giving my post a LIKE. Would love you to subscribe - it is entirely free to do so and I plan to keep it that way.
Other material:
e - Euler's number (mathsisfun.com)
Exponential Growth and Decay (mathsisfun.com).
Calculating Euler’s Constant (e) - Maths Careers
e (mathematical constant) - Wikipedia
Interest – Simple and Compound - BBC Bitesize
Compound Interest Formula - Overview, How To Calculate, Example (corporatefinanceinstitute.com)
Radioactive decay
Decay graphs and half lives article (article) | Khan Academy
EulerPresentation (uky.edu) - looks at the life and work of Euler.
These are easily calculated using an Exponent Calculator - e.g. https://www.omnicalculator.com/math/exponent