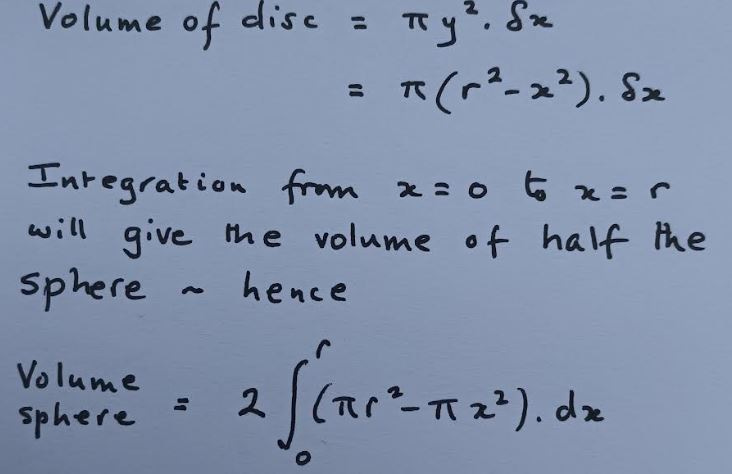Archimedes and the Volume of the Sphere
Cones, Spheres, Cylinders, Archimedes Principle, Law of Levers
In the Viewpoint on Pyramids it was shown that the Volume of a Cylinder with a base of radius R and vertical height H is πR2H. Also, the Volume of a Pyramid is 1/3 x Area of Base x Vertical height and the volume of a Cone is 1/3 x πR2H.
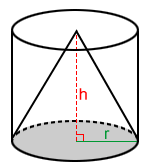
If the cone is inscribed within a cylinder (as in the diagram) it follows that the volume of the cone is one-third that of the cylinder.
Another object that can be imagined to fit neatly within a cylinder is a SPHERE (of radius R but what is the volume of such a sphere?
The answer was first deduced by Archimedes (c. 287 to 211 BCE) who also set out the famous ‘Archimedes Principle’ that the upward buoyant force exerted on a body immersed in a fluid, whether wholly or partially submerged, is equal to the weight of the fluid that the body displaces.
Any particular fluid (e.g. water) has a density - that is, weight per unit volume which, for water, is basically one gram per cubic centimetre.1 Hence, it can also be stated that the volume of displaced fluid is equivalent to the volume of an object fully immersed in the fluid or to that fraction of the volume below the surface for an object partially submerged in the liquid.
It may be that Archimedes applied that principle to deduce the volume of a sphere. He probably obtained three solid objects made from the same material: a cylinder of base radius R and height 2R, a cone with base radius R and height 2R, and finally a sphere of radius R
The cylinder was fully immersed in water and the volume of water displaced was measured. Next, the cone and the sphere were placed together in the water and the volume displaced measured. It was found that:
Volume Cylinder = Volume cone + Volume Sphere
so
Volume Sphere = Volume Cylinder - Volume cone
The cylinder volume is πR2.2R = 2πR3
The cone (of height 2R) has volume 1/3.πR2 x 2R = 2/3.πR3
Hence Volume Sphere = 2πR3 - 2/3.πR3 = 4/3πR3
The same result is sometimes illustrated using a “double nappe cone” and that approach is shown in this short video - The Volume of a Sphere - Numberphile - YouTube
When the volumes are compared, an interesting relationship appears between the volume of a cylinder and the volumes of a cone and a sphere inscribed within the cylinder. The cone volume is one-third that of the cylinder. The sphere volume is two-thirds that of the cylinder. Cone vs Sphere vs Cylinder (mathsisfun.com)
Another approach:
Archimedes reportedly said - ‘Give me a place to stand and I will move the earth’
He was referring to the use of levers.
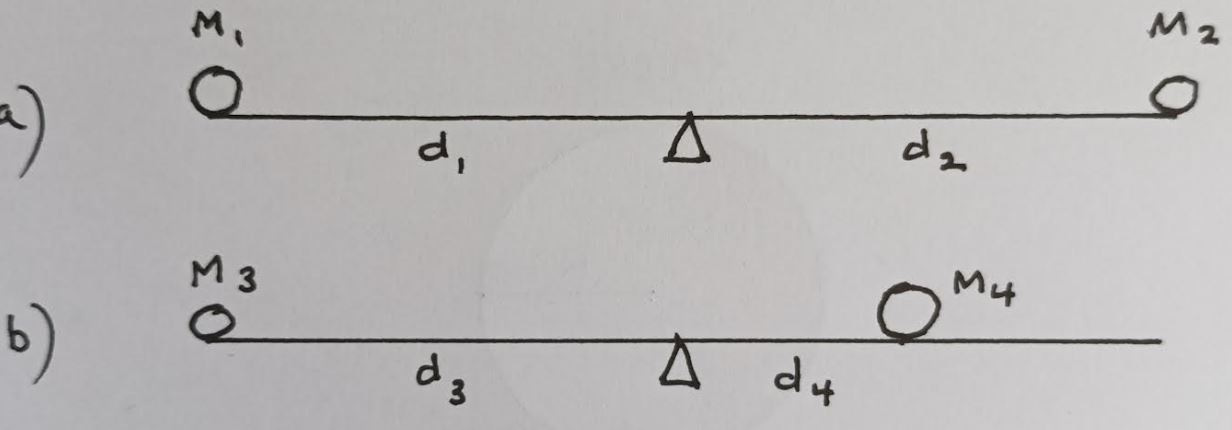
The diagram (a) shows a beam (seesaw) with weights M1 and M2 on it at distances d1 and d2 from the “fulcrum”
The beam is level (or balanced) when the ‘moments’ created by the weights are equal. That is when
M1d1 = M2d2
In the diagram (b), weight M4 is twice weight M3
Therefore, to achieve balance, M4 has to be placed half the distance (d4)from the fulcrum than the distance (d3) of weight M3
This “law of levers” was developed by Archimedes to deduce the Volume of a Cone. The method is shown in this video.
Calculus:
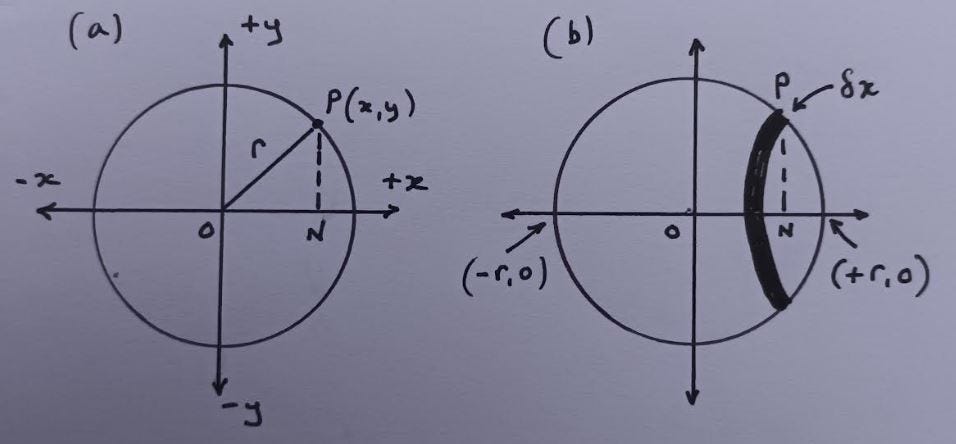
In modern times, integral calculus would usually be used to find the volume of a sphere.2 The next diagram (a) shows a point (P) on a circle centred at the origin (O) of a cartesian coordinate system. The circle has radius r. Applying the Pythagorean Theorem
OP2 = ON2 + NP2
or
r2 = x2 + y2
Hence
y2 = r2 - x2
The diagram (b) shows a sphere generated by rotating the circle about the x-axis. At point P is a disc with a very small thickness δx
The volume of that disc is πy2.δx
Since y2 = r2 - x2 we can write Volume of disc = π(r2 –x2).δx
Once the volume of the very small disc is expressed in terms of x, we can integrate the expression to obtain the volume of the sphere. As shown in this next image, integration from x = 0 to x = r will give half the volume of the sphere so it is then only necessary to double the result to get the volume of the whole sphere.3
From there we get the Volume of the sphere to be
Archimedes Principle - video
Fluids, Buoyancy, and Archimedes' Principle (youtube.com)
Archimedes’ principle | Description & Facts | Britannica
Levers - videos
Additional Materials
An excellent video (with superb graphics) by MATHOLOGER asks Why are the formulas for the sphere so weird? (major upgrade of Archimedes' greatest discoveries) - (youtube.com). This video also touches upon “Equal Area” map projections
A spectacular landmark in the history of mathematics was the discovery by Archimedes (287-212 B.C.) that the volume of a solid sphere is two thirds the volume of the smallest cylinder that surrounds it, and that the surface area of the sphere is also two-thirds the total surface area of the same cylinder. Archimedes was so excited by this discovery that he wanted a sphere and its circumscribing cylinder engraved on his tombstone, even though there were many other great accomplishments for which he would be forever remembered. He made this particular discovery by balancing slices of a sphere and cone against slices of a larger cylinder, using centroids and the principle of the lever, which were also among his remarkable discoveries. See the article by Tom A Apostol and Mamikon A Mnatsakanian - A Fresh Look at the Method of Archimedes.
Archimedes discovers the Volume of a Sphere (weber.edu)
Archimedes on Mechanical and Geometric Methods
The Archimedes Palimpsest and The Guardian Archimedes Palimpsest reveals insights centuries ahead of its time. (A palimpsest is a manuscript page, either from a scroll or a book, from which the text has been scraped or washed off in preparation for reuse in the form of another document. Parchment was made of lamb, calf, or kid skin and was expensive and not readily available, so, in the interest of economy, a page was often re-used by scraping off the previous writing).
On the Sphere and Cylinder - (by Archimedes)
The Method of Mechanical Theorems - Wikipedia
Equal Area Projection Maps in Cartography - GIS Geography
What Is the Density of Water? By Temperature and Unit (prepscholar.com)
Youtube has several videos on this but I hope my text is clear enough to show the method.
Alternatively, integrate from -r to +r and the volume of the whole sphere is obtained. The approach shown above is somewhat simpler.